Contents.The algorithm Booth's algorithm examines adjacent pairs of of the 'N'-bit multiplier Y in signed representation, including an implicit bit below the, y −1 = 0. For each bit y i, for i running from 0 to N − 1, the bits y i and y i−1 are considered. Where these two bits are equal, the product accumulator P is left unchanged. Where y i = 0 and y i−1 = 1, the multiplicand times 2 i is added to P; and where y i = 1 and y i−1 = 0, the multiplicand times 2 i is subtracted from P. The final value of P is the signed product.The representations of the multiplicand and product are not specified; typically, these are both also in two's complement representation, like the multiplier, but any number system that supports addition and subtraction will work as well. As stated here, the order of the steps is not determined.

1. Algorithm In C
2. C++ Program Download
3. Advantages Of Booth's Algorithm

Algorithm In C

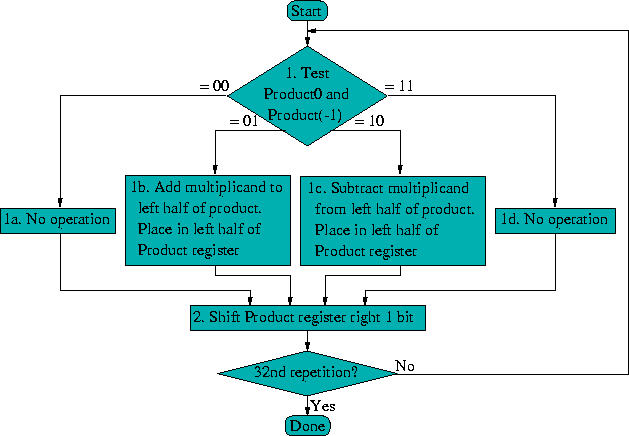
Typically, it proceeds from to, starting at i = 0; the multiplication by 2 i is then typically replaced by incremental shifting of the P accumulator to the right between steps; low bits can be shifted out, and subsequent additions and subtractions can then be done just on the highest N bits of P. There are many variations and optimizations on these details.The algorithm is often described as converting strings of 1s in the multiplier to a high-order +1 and a low-order −1 at the ends of the string. When a string runs through the MSB, there is no high-order +1, and the net effect is interpretation as a negative of the appropriate value.A typical implementation. (1951) 1950-08-01.

The Quarterly Journal of Mechanics and Applied Mathematics. IV (2): 236–240. (PDF) from the original on 2018-07-16.

Retrieved 2018-07-16. Reprinted in. A Signed Binary Multiplication Technique. Pp. 100–104. Chen, Chi-hau (1992). P. 234.Further reading.

Collin, Andrew (Spring 1993). London: (5).; (1998). (Second ed.). San Francisco, California, USA:. (2000). New Jersey:. Savard, John J.

(2018) 2006. From the original on 2018-07-03. Retrieved 2018-07-16.External links. in.

C++ Program Download

Lexicographically minimal string rotation or lexicographically least circular substring is the problem of finding the rotation of a string possessing the lowest lexicographical order of all such rotations.For example, the lexicographically minimal rotation of bbaaccaadd would be aaccaaddbb. It is possible for a string to have multiple lexicographically minimal rotations, but this does not matter as the rotations must be equivalent.The idea is to iterate through successive rotations of the given string while keeping track of the most lexicographically minimal rotation encountered. Below is C and Java implementation of the idea –. Output:The lexicographically minimal rotation of bbaaccaadd is aaccaaddbbThe time complexity of above solution is O(n 2) and auxiliary space used by the program is O(1).can solve this problem in O(n ) time. The algorithm uses a modified preprocessing function from the Knuth-Morris-Pratt string search algorithm. The failure function for the string is computed as normal, but the string is rotated during the computation so some indices must be computed more than once as they wrap around. Once all indices of the failure function have been successfully computed without the string rotating again, the minimal lexicographical rotation is known to be found and its starting index is returned.

Advantages Of Booth's Algorithm

We will be soon discussing implementation of Booth’s Algorithm.